Logical Constraints

Whereas a fact allows you to say what is always true, and a rule allows you to say what is sometimes true, a logical constraint allows you to say what is never true.

For a small example, imagine we have a situation where there are people, people have ages, there is a person called bob, and bob has the age 40, and bob has the age 50.

This naturally doesn't make a lot of sense, because we understand that ages are a thing that people do not usually have more than one of.

Right now, if we asked what age Bob is, we would get two answers. If we preferred that Blawx should treat any situation in which a person has two ages as a logically invalid scenario, which should never return an answer, we can create a logical constraint. If all of the elements of a logical constraint are true in a model, that model will never be returned as an answer to a query.

Note that this is not the same as saying "we want people to only have one age". What it means is that "if a person has two ages, I don't want any answers at all."

We could implement that by imposing a logical constraint that says a person can only have one age, like this:

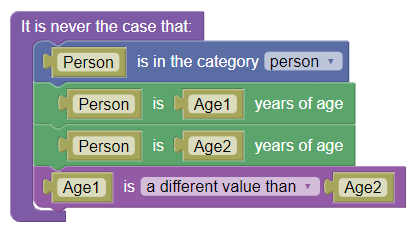
Now, if you run the query "do any people have any age", you will get no models, because the only person with an age violates the constraint. If you then disable the logical constraint, the same query will answer that bob has the age 40 and bob has the age 50. If you keep the constraint, but get rid of the ages, the same query will answer whatever single age you have left in the code.

Working with Logical Constraints

Note that a logical constraint has the effect of making the code "inconsistent" when all of its conditions are true. If you have a number of constraints, and your code is unexpectedly returning "no models", one of those constraints is probably being violated, but it might be difficult to tell which. This means that working with logical constraints can make your code harder to debug.

It may be easier to create an object with a property that is set to true if the conditions are met, and a single constraint that this value cannot be true. Then, when you believe a constraint is being violated, you can disable the only constraint block, and query whether that value is true, and get an explanation for why. This will make it a lot easier to debug problems with constraints.

Note also that constraints can incur a considerable speed penalty depending on your code. If it is possible to do what you want to do without using constraint blocks, that may improve the speed of your code.